The 2-link manipulator is a fundamental robotics system that is used by robot enthusiasts to understand the principles of kinematics. A 2-link manipulator consists of two rigid links connected by revolute joints, allowing for planar motion.
In this post, we will explore the forward and inverse kinematics of a 2-link manipulator.
Forward kinematics - Given joint parameters, what is the position of the end-effector
Inverse kinematics - Given the position of the end-effector, what are the joint parameters
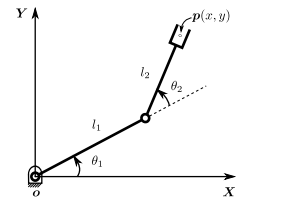
In the above diagram,
- Joint parameters:
- \(\theta_1, \theta_2\)
- Link parameters:
- \(l_1, l_2\)
- End-effector position:
- \(x, y\)
Forward Kinematics
The forward kinematics of 2-link manipulators is highly intuitive using geometry.
$$ x = l_1cos(\theta_1) + l_2cos(\theta_1 + \theta_2) $$$$ y = l_1sin(\theta_1) + l_2sin(\theta_1 + \theta_2) $$Inverse Kinematics
Let \(\phi = \theta_1 + \theta_2\)
By geometry we know that,
$$ tan(\phi) = y/x$$$$ \phi = Atan2(y, x) $$Now, if we square and add both the forward kinematic equations.
We get:
Now, that we know \(\theta_2\)
$$ \theta_1 = \phi - \theta_2 $$And, that’s it. Both forward kinematics and inverse kinematics equations are derived.