DES is a symmetric-key block cipher that follows the Fiestal Cipher structure.
The steps involved in encryption are:
- Apply an initial permutation to the 64-bit input block using a permutation matrix
- Similar to the Fiestal Cipher structure, split the 64 bit output after permutation into 2 halves \(L_0\) (32 bits) and \(R_0\) (32 bits)
- Compute F(\(R_0\), \(k_0\)) using expansion, XOR, S-boxes, and permutation
- Set \(L_1\) = \(R_0\) and \(R_1\) = \(L_0\) XOR F(\(R_0\), \(k_0\))
- Now, this concludes the first round. Now, do steps 3-4 15 more times
- After round 16, perform a 32-bit swap like in Fiestal Cipher structure
- Undo the initial permutation to get the cipher text
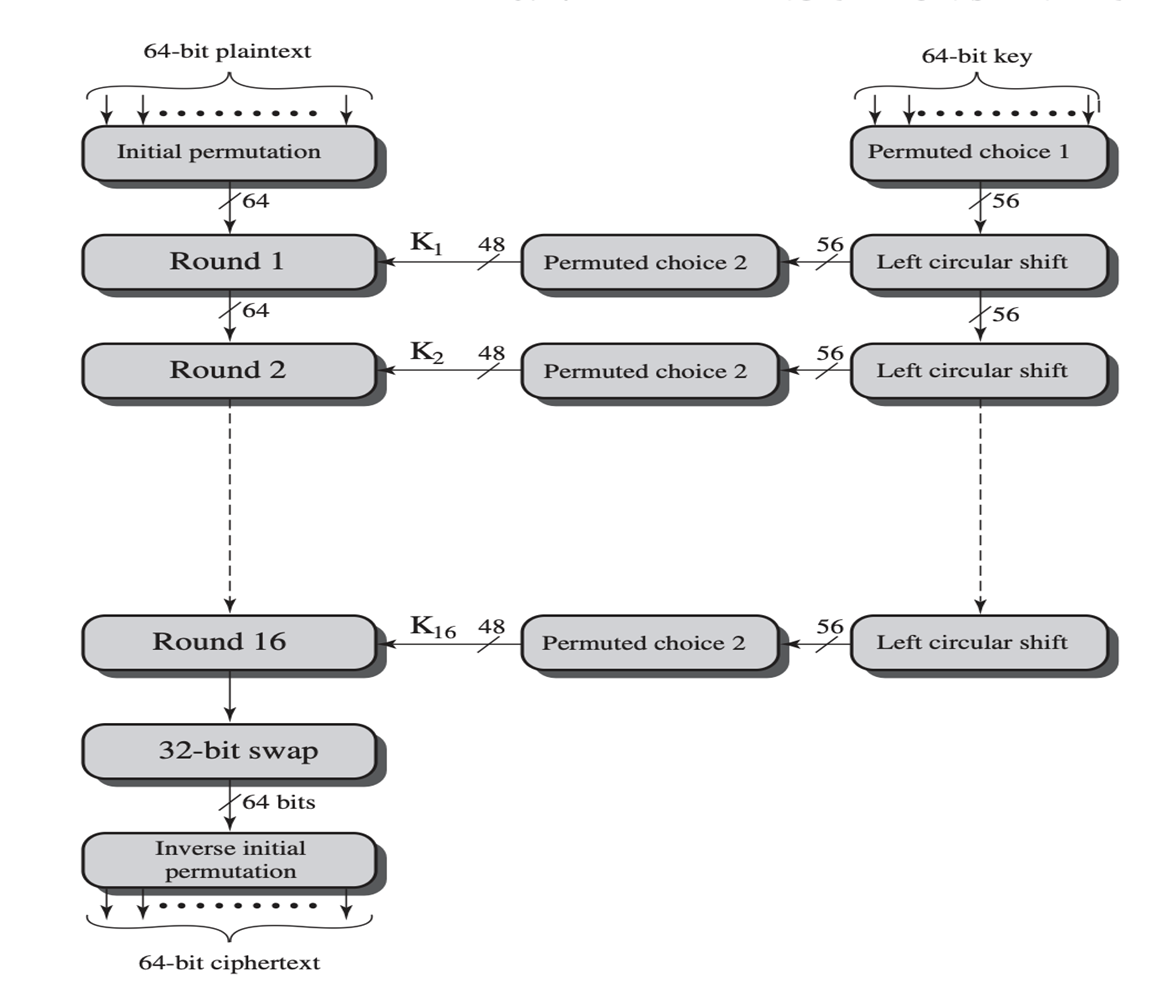
The above figure illustrates the DES encryption workflow.
Now, let’s look at some of the non-intuitive steps in detail:
Initial Permutation
This step involves transposition of the 64-bit input block based on a IP matrix. The \(IP^{-1}\) matrix is the reverse of the IP matrix which will be used in the last step will undo this transposition. This permutation plays no role in the cryptography aspect of the cipher. This step was introduced because of hardware considerations which were a major bottleneck during the 20th century.
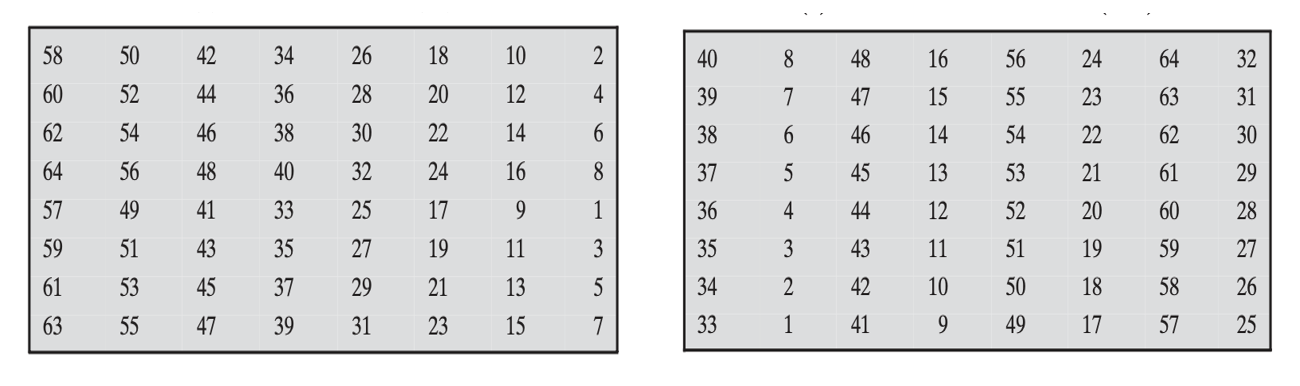
The above table illustrates the initial permutation matrix and the reverse initial permutation matrix.
The Fiestal Function (F)
The heart of DES encryption lies in its Fiestal Function F, which takes two inputs: a 32-bit right half of data (\(R_i\)), and a 48-bit round key (\(k_i\)). The Fiestal Function provides DES the 2 key principles of encryption:
- Diffusion (The influence of 1 input bit should be spread across multiple output bits)
- Confusion (The relationship between input and output is hidden)
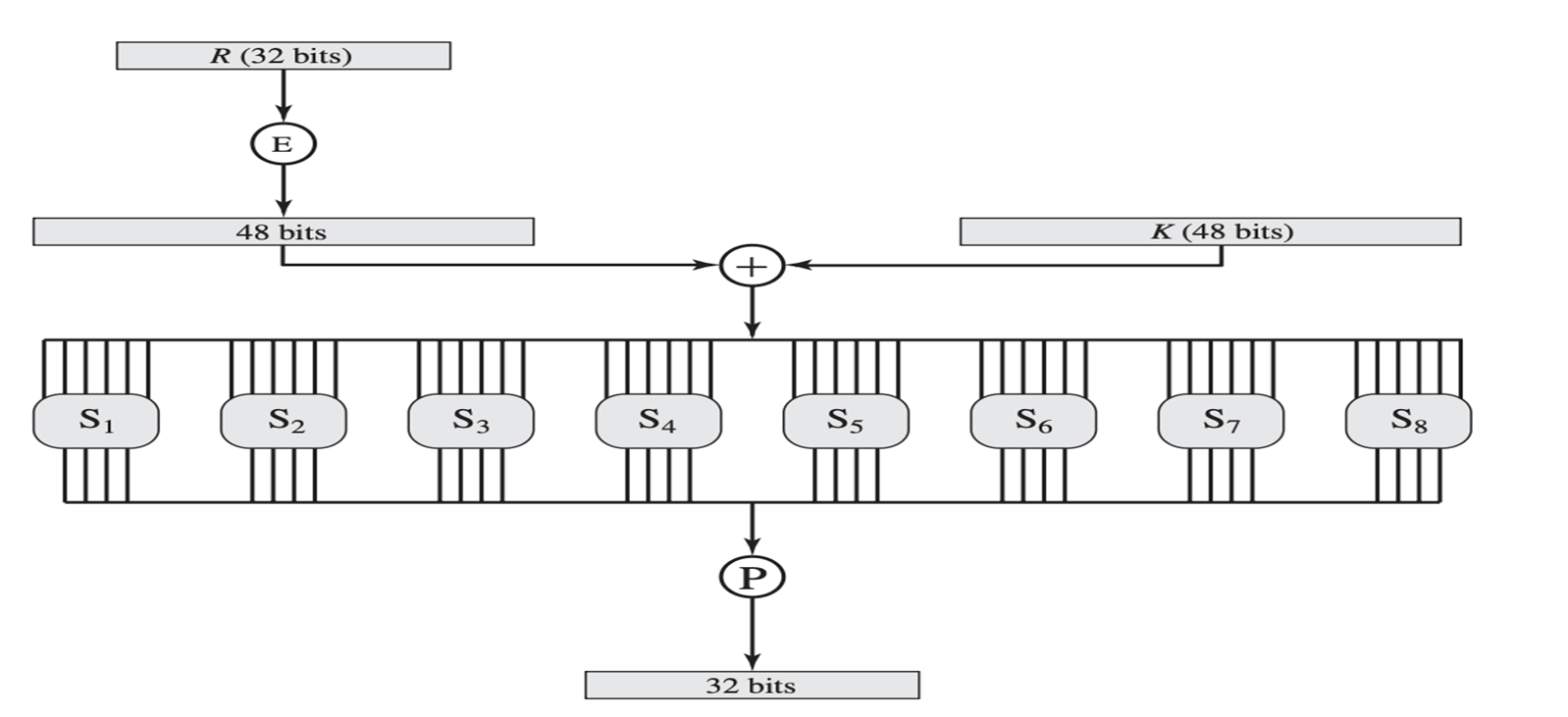
The figure above illustrates the Fiestal function workflow.
There are 4 steps involved in the Fiestal Function:
- Expansion (E-box)
The expansion provides Diffusion. Expansion ensures diffusion by duplicating 16 of input bits in the output. Thus, the 32 bit \(R_i\) input is expanded to a 48 bit output by duplicating 16 bits in the input.
32 bit -> E-box -> 48 bit
This idea is illustrated below:
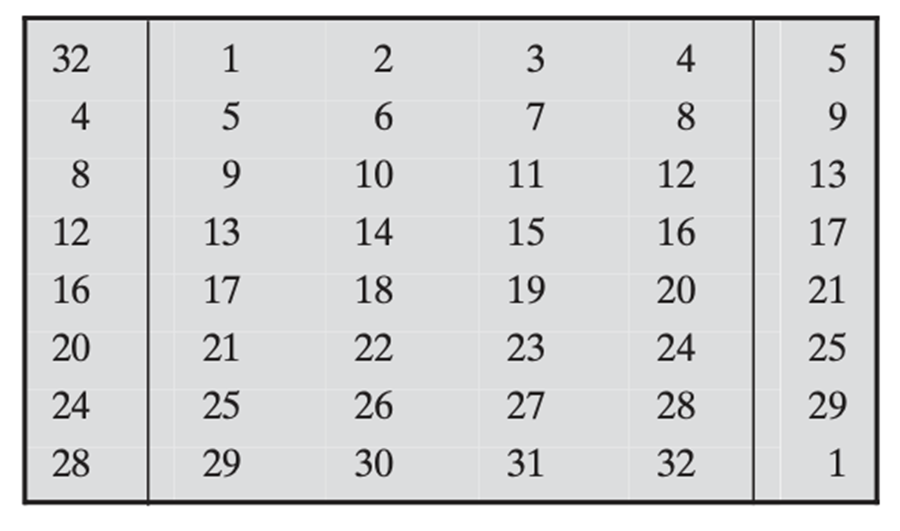In the above table, the first and the last column contain the repeated bits of the input.
- XOR with subkey (\(k_i\)) This step is pretty straight forward.
E-box output (48 bit) XOR Sub-key (\(k_i\))= 48 bit Output
- Substitution (S-box)
The substitution provides Confusion. This is one of the crucial parts of the encryption process as this ensures that there is a complex relationship between the plain text and the cipher text.
Steps involved:- The 48-bit result from the XOR operation is divided into eight 6-bit chunks
- Each chunk is processed by its own S-box (4x16 matrix), which takes 6 bits as input, and outputs 4 bits
- The first and last bits choose one of the 4 possible rows, and the middle 4 bits select one of the 16 possible columns
- Using the row and column, choose the 4-bit entry from substitution lookup table
- For each of the 8 chunks, you get a 4-bit entry. Therefore, the overall output will be 32 bits long.
The above table is an example of a substitution lookup table
- Permutation (P-box)
The final step applies a permutation to the 32-bit output from the S-boxes. This permutation rearranges the bits further contributing to diffusion by ensuring the current output of the S-box affects multiple S-boxes in next rounds.
Reverse Permutation
This step involves undoing the intitial permutation to get the final cipher text using \(IP^{-1}\)
Round Key Generation
The 16 subkeys (\(k_0\) to \(k_{15}\)) used in each round are derived from the original 64-bit key using a key schedule algorithm. The key schedule involves:
- Initial Permutation : The original 64-bit key undergoes a permutation that reduces it to 56 bits by discarding every 8th bit (used for parity).
- Splitting: The 56-bit key is divided into two 28-bit halves.
- Left Shifts: Each half is subjected to a series of left shifts (1 or 2 bits) depending on the round number.
- Compression Permutation : The shifted halves are combined and permuted to produce a 48-bit subkey for the round.
- This process is repeated for all 16 rounds to generate the required subkeys.